いや~突然訪れた長~い春休み。さすがに二人のボーイズを放置しとくと毎日ゲーム三昧でやっばい。
たまにはお勉強させないといかん!ということで兄ボーイ(もうすぐ中学1年生)が算数ドリルをやってるの見てたら、ちょっと…。これやばくね?ということに。

ちょっと明日から父ちゃん一緒に勉強みるよ!(悲しいことに仕事が暇だから)毎日これやろう!
今までもたまに宿題をみてるとき、「これであってるんだよな(不安…)」みたいなことが多々あったので、一応予習してみよっかな〜と軽い気持ちでドリルをみてみる。
繰り返し計算ドリル6年3学期
うちの兄ボーイが使ってるドリルはスヌーピーが表紙のこれ。
「新版くりかえし計算ドリルワイド」教育同人社

「比の性質」の問題 9:3=x:4
お父さんの予習であれ?となった問題がこれ。
9:3=x:4
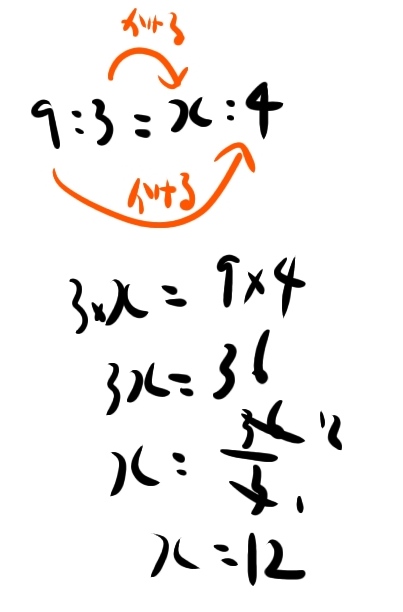

おーっ、これならわかるぞ。「内側×内側=外側×外側」だな。
内側(3)かける内側(X)=外側(9)かける外(4)
だから、
3×X=9×4
3X=36
x=12
だよね!おーお父さんでも出来ちゃう〜。らくしょー(安堵)!
と思って答えをみてみると、
9×4/3(3分の4)=12
と出ている。答えは一緒だけでどあれ?なんでいきなし9に4/3をかけてるんだ?
もしかして内×内=外×外って中学生の解き方?

これはやばい(汗)
教科書を見てみないと…。ふんふん比の値…。
比の値
比の値
a:bの比で、bをもとにしてaがどれだけの割合になるかを表したものを、a:bの比の値といいます。
教科書
a:bの比の値は、aをbでわった商になります。

え〜っとこの比の値で考えて行けばいいのかな…(不安)。
問題 9:3=X:4
左側 9:3の比の値は9/3(3分の9)で、
右側 x:4=X/4(4分のX)
だから、
9/3=X/4
X=12
まあこれでも良さそうな気がするけど…。答えはいきなり9×4/3だからな。
もうちょっと教科書をみてみると…。これだ。
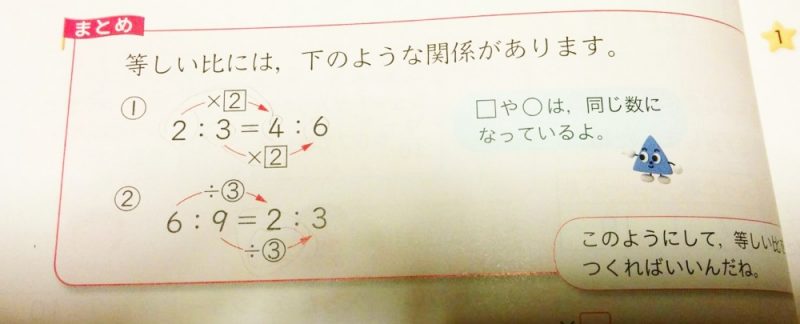
等しい比には、下のような関係があります。
教科書

なるほど…。
2:3という比を表すそれぞれの数字に、同じ数をかけたり割ったりしても比の値は変わりません。
小学校算数のわかりやすい教え方
ということで、問題をもう一度。
問題 9:3=X:4

3になにかをかけて4にしたい。
3かける4/3(3分の4)=4になるから、
9×4/3(3分の4)=12
ということだね。これむずかしいな(汗)。
兄ボーイは分数もやばそうだから3×□=4をつくれるのだろうか…。
これは内内外外を覚えろと言い放ってよいのだろうか…。
実際に兄ボーイがやってみた。

あ〜これやった。どーやんだっけなあ〜。

これだぞ。


ああ。3を4にすればいいのか。
??3を4???は?

…。3に何かをかけて、4にするんだゾ。ヒントは分数…。

えーっと3分の1かな。

(マジかよ…)じゃあかけてみなよ。

3×3分の1は…えーっと1。
あれ?じゃあちがうな…。えーっとわかった!
3分の4か。ってことは12だな。

そおッ!それだっ!(かなり不安だけど)できたじゃああん!
これは、なかなか大変そうだぞ。分数の計算と小数点の割り算も復習したい…。でも、とりあえず毎日1ページずつやっていこう。この春休み。